Understanding and predicting the dynamics of complex systems
Describing the dynamics of complex systems is both important and challenging. Such systems encompass a wide range of phenomena, including neurological processes in the brain (see above), the spread of novel viruses, the behavior of AI agents, climatic developments, and cellular processes such as division, which may lead to cancerous growth or rejuvenation.
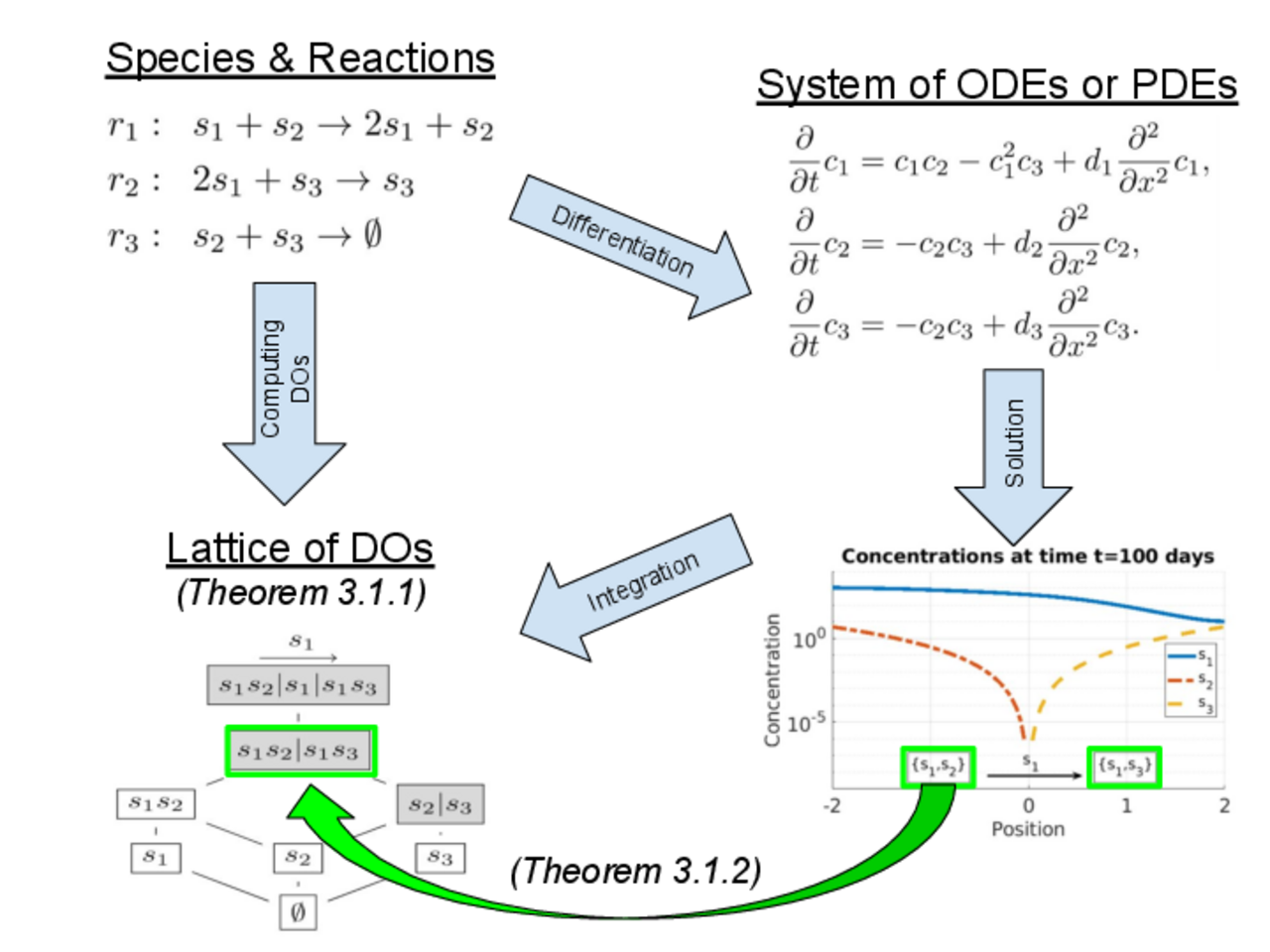
A theoretical framework from systems and network theory—introduced in a SIAM article titled "Linking network structure and dynamics to describe the set of persistent species in reaction-diffusion systems“—offers mathematically rigorous tools for identifying all long-term persistent subsystems, even within highly complex systems.
This theory was recently extended, and an efficient algorithm was presented in a paper published in Nature Scientific Reports, titled "Computing all persistent subspaces of reaction-diffusion system."
Typical application domains include cell cycle dynamics, microbial ecosystems, neurological signaling pathways, and virus infection dynamics (see below).
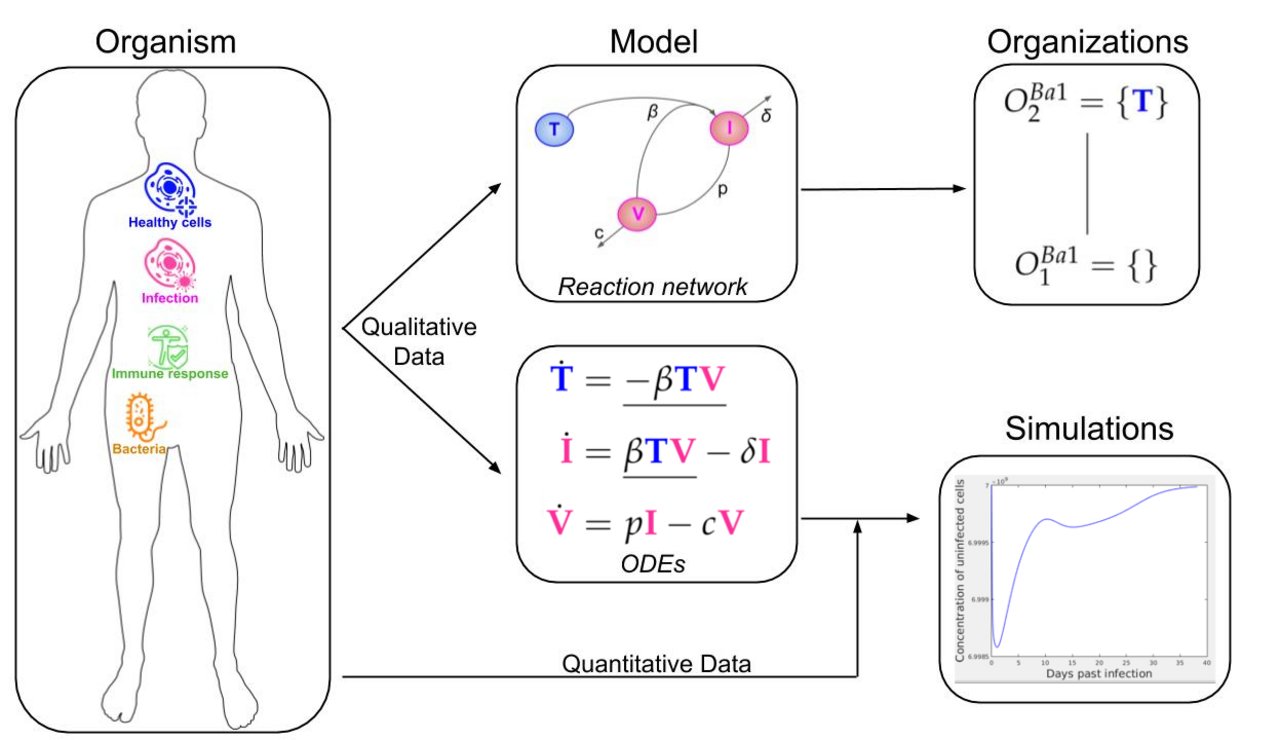
Virus infection dynamics
Mathematical models of virus infection dynamics are essential for understanding the progression of infections, optimizing treatment strategies, and guiding vaccine development.
We applied the organization theory outlined above to infection models of Influenza A and SARS-CoV-2.
This approach enabled us to identify and characterize a wide range of model types using a rigorous mathematical framework.
Our findings may contribute to the construction and analysis of more sophisticated models in the future.
